This tutorial shows how to use Tensorflow to create a neural network that mimics 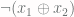 function. This function, abbreviated as XNOR, returns 1 only if
function. This function, abbreviated as XNOR, returns 1 only if 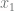 is equal to
is equal to 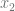 . The values are summarized in the table below:
. The values are summarized in the table below:

Andrew Ng shows in Lecture 8.5: Neural Networks – Representation how to construct a single neuron that can emulate a logical AND operation. The neuron is considered to act like a logical AND if it outputs a value close to 0 for (0, 0), (0, 1), and (1, 0) inputs, and a value close to 1 for (1, 1). This can be achieved as follows:
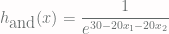
To recreate the above in tensorflow we first create a function that takes theta, a vector of coefficients, together with x1 and x2. We use the vector to create three constants, represented by tf.constant. The first one is the bias unit. The next two are used to multiply x1 and x2, respectively. The expression is then fed into a sigmoid function, implemented by tf.nn.sigmoid.
Outside of the function we create two placeholders. For Tensorflow a tf.placeholder is an operation that is fed data. These are going to be our x1 and x2 variables. Next we create a h_and operation by calling the MakeModel function with the coefficient vector as suggested by Andrew Ng.
def MakeModel(theta, x1, x2):
h = tf.constant(theta[0]) + \
tf.constant(theta[1]) * x1 + tf.constant(theta[2]) * x2
return tf.nn.sigmoid(h)
x1 = tf.placeholder(tf.float32, name="x1")
x2 = tf.placeholder(tf.float32, name="x2")
h_and = MakeModel([-30.0, 20.0, 20.0], x1, x2)
We can then print the values to verify that our model works correctly. When creating Tensorflow operations, we do not create an actual program. Instead, we create a description of the program. To execute it, we need to create a session to run it:
with tf.Session() as sess:
print " x1 | x2 | g"
print "----+----+-----"
for x in range(4):
x1_in, x2_in = x & 1, x > 1
print " %2.0f | %2.0f | %3.1f" % (
x1_in, x2_in, sess.run(h_and, {x1: x1_in, x2: x2_in}))
The above code produces the following output, confirming that we have correctly coded the AND function:
x1| x2 | g
----+----+-----
0 | 0 | 0.0
0 | 1 | 0.0
1 | 0 | 0.0
1 | 1 | 1.0
To get a better understanding of how a neuron, or more precisely, a sigmoid function with a linear input, emulates a logical AND, let us plot its values. Rather than just using four points, we compute its values for a set of 20 x 20 points from the range [0, 1]. First, we define a function that, for a given input function (a tensor) and a linear space, computes values of returned by the function (a tensor) when fed points from the linear space.
def ComputeVals(h, span):
vals = []
with tf.Session() as sess:
for x1_in in span:
vals.append([
sess.run(h, feed_dict={
x1: x1_in, x2: x2_in}) for x2_in in span
])
return vals
This is a rather inefficient way of doing this. However, at this stage we aim for clarity not efficiency. To plot values computed by the h_and tensor we use matplotlib. The result can be seen in Fig 1. We use coolwarm color map, with blue representing 0 and red representing 1.

Fig 1. Values of a neuron emulating the AND gate
Having created a logical AND, let us apply the same approach, and create a logical OR. Following Andrew Ng’s lecture, the bias is set to -10.0, while we use 20.0 as weights associated with x1 and x2. This has the effect of generating an input larger than or equal 10.0, if either x1 or x2 are 1, and -10, if both are zero. We reuse the same MakeModel function. We pass the same x1 and x2 as input, but change vector theta to [-10.0, 20.0, 20.0]
h_or = MakeModel([-10.0, 20.0, 20.0], x1, x2)
or_vals = ComputeVals(h_or, span)
When plotted with matplotlib we see the graph shown in Fig 2.

Fig 2. Values of a neuron emulating the OR gate
The negation can be crated by putting a large negative weight in front of the variable. Andrew Ng’s chose  . This way
. This way 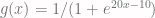 returns
returns  for
for 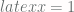 and
and 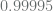 for
for  . By using −20 with both
. By using −20 with both x1 and x2 we get a neuron that produces a logical and of negation of both variables, also known as the NOR gate:  .
.
h_nor = MakeModel([10.0, -20.0, -20.0], x1, x2)
nor_vals = ComputeVals(h_nor, span)
The plot of values of our h_nor function can be seen in Fig 3.
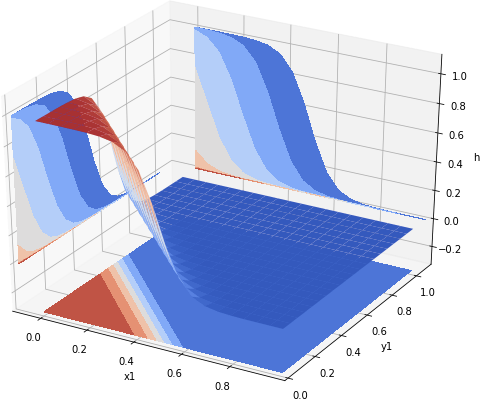
Fig 3. Value of a neuron emulating the NOR gate
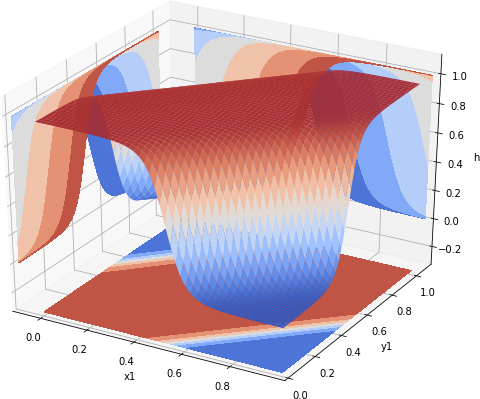
With the last gate, we have everything in place. The first neuron generates values close to one when both x1 and x2 are 1, the third neuron generates value close to one when x1 and x2 are close to 0. Finally, the second neuron can perform a logical OR of values generated from two neurons. Thus our xnor neuron can be constructed by passing h_and and h_nor as inputs to h_or neuron. In Tensorflow this simply means that rather than passing x1 and x2 placeholders, when constructing h_or function, we pass h_and and h_nor tensors:
h_xnor = MakeModel([-10.0, 20.0, 20.0], h_nor, h_and)
xnor_vals = ComputeVals(h_xnor, span)
Again, to see what is happening, let us plot the values of h_xnor over the [0, 1] range. These are shown in Fig 4.

Fig 4. Value of a neural net emulating XNOR gate
In a typical Tensorflow application we would not see only constants being used to create a model. Instead constants are used to initialize variables. The reason we could use only constants is that we do not intend to train the model. Instead we already knew, thanks to Andrew Ng, the final values of all weights and biases.
Finally, the solution that we gave is quite inefficient. We will show next how by vectorising it one can speed it up by a factor of over 200 times. This is not an insignificant number, considering how simple our model is. In larger models vectorization can give us even more dramatic improvements.
Resources
You can download the Jupyter notebook from which code snippets were presented above from github xnor-basic repository.













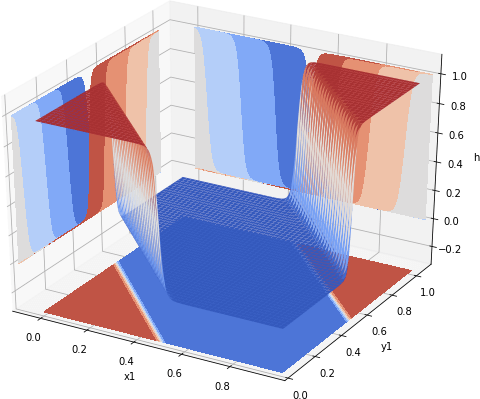
 Fig 1. Data flow graph as rendered by tensorboard
Fig 1. Data flow graph as rendered by tensorboard